等效轉動慣量專用HD執行元件SHA40A-121SG-B15A200V-10S17B-C(Moment of Inertia)是剛體繞軸轉動時慣性（回轉物體保持其勻速圓周運動或靜止的特性）的量度，用字母I或J表示。轉動慣量在旋轉動力學中的角色相當于線性動力學中的質量，可形式地理解為一個物體對于旋轉運動的慣性，用于建立角動量、角速度、力矩和角加速度等數個量之間的關系。

等效轉動慣量專用HD執行元件SHA40A-121SG-B15A200V-10S17B-C(Rotational Inertia)是剛體轉動時慣性的量度，其量值取決于物體的形狀、質量分布及轉軸的位置。剛體的轉動慣量有著重要的物理意義，在科學實驗、工程技術、、電力、機械、儀表等工業領域也是一個重要參量。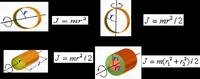電磁系儀表的指示系統，因線圈的轉動慣量不同，可分別用于測量微小電流（檢流計）或電量（沖擊電流計）。在發動機葉片、飛輪、陀螺以及人造衛星的外形設計上，精確地測定轉動慣量，都是十分必要的。

對于質量分布均勻，外形不復雜的物體可以從它的外形尺寸的質量分布用公式計算出相對于某一確定轉軸的轉動慣量。對于幾何形狀簡單、質量分布均勻的剛體可以直接用公式計算出它相對于某一確定轉軸的轉動慣量。而對于外形復雜和質量分布不均勻的物體只能通過實驗的方法來精確地測定物體的轉動慣量，因而實驗方法就顯得更為重要。

等效轉動慣量專用HD執行元件SHA40A-121SG-B15A200V-10S17B-CRotational Inertia剛體繞軸轉動慣性的度量。其數值為J=∑ mi*ri^2，式中mi表示剛體的某個質點的質量，ri表示該質點到轉軸的垂直距離。

求和號（或積分號）遍及整個剛體。轉動慣量只決定于剛體的形狀、質量分布和轉軸的位置，而同剛體繞軸的轉動狀態（如角速度的大小）無關。形狀規則的均質剛體，其轉動慣量可直接計得。不規則剛體或非均質剛體的轉動慣量，一般用實驗法測定。轉動慣量應用于剛體各種運動的動力學計算中。

描述剛體繞互相平行諸轉軸的轉動慣量之間的關系，有如下的平行軸定理：剛體對一軸的轉動慣量，等于該剛體對同此軸平行并通過質心之軸的轉動慣量加上該剛體的質量同兩軸間距離平方的乘積。由于和式的項恒大于零，因此剛體繞過質量中心之軸的轉動慣量是繞該束平行軸諸轉動慣量中的最小者。

轉動慣量嚴格來說是一個張量，必須從張量的角度對其進行定義。出于簡單的角度考慮，這里僅給出繞質心的轉動慣量張量的定義及其在力矩方程中的表達.

設有一個剛體A,其質心為C,剛體A繞其質心C的轉動慣量張量定義為Jc，則Jc=∫ρ(r●rδ-rr)dV。該積分遍及整個剛體A，且，

等效轉動慣量專用HD執行元件SHA40A-121SG-B15A200V-10S17B-C其中，r=r1 e_1 + r2 e_2 + r3 e_3 ，是剛體質心C到剛體上任一點B的矢徑；表達式rr是兩個矢量的并乘；而單位張量δ是度量張量，δ=δ_ij e_i e_j ，這里i和j是啞指標，標架(C;e_1，e_2，e_3)是一個典型的單位正交曲線標架；ρ是剛體的密度。

設剛體A所受到的繞其質心C的合力矩矢量為ΣMc，剛體A在慣性系下的角速度矢量為ω，角加速度矢量為α，A繞其質心的轉動慣量張量為Jc，則有如下的力矩方程：

ΣMc=Jc●α+ω×Jc●ω

將上面的矢量形式的力矩方程向各個坐標軸投影（或者，更確切地說，與各個坐標軸的單位方向矢量相點乘），就可以獲得各個坐標軸分量方向的標量形式的力矩方程。

等效轉動慣量專用HD執行元件SHA40A-121SG-B15A200V-10S17B-C轉動慣量張量Jc是一個二階張量，雖然在標架(C;e_1，e_2，e_3)下它有九個分量，但是因為它是一個對稱張量，故其實際獨立的分量只有六個。